本网讯 (黄石市广州路小学 张强) 在四年级下册教学中，学生已经掌握了三角形内角和为180°，因此，教师引导学生探究多边形内角和时，要引导学生运用转化的策略，化繁为简，化难为易，将多边形分成若干个三角形，这若干个三角形内角之和就是多边形的内角和，从而归纳出一般的规律，总结出多边形内角和公式，解决多边形内角和相关问题。

在本课教学中，可以采用以下教学过程。

一、分析特例，猜想规律。

1.提出问题，引发思考。学生拿出一个正方形纸片，一个平行四边形纸片，同桌互相说一说这几个图形的内角和。提问：你能联想到他们的内角和是多少？由此可以引发学生的思考，四边形内角和都等于360度吗？五边形，六边形，七边形的内角和又是多少呢？

2.分析问题，提炼思路。你应该怎样探究多边形的内角和呢？（以四边形为例）

方法一：测量法。用量角器量出四边形的每个角，再将他们度数之和求出来。

方法二：剪拼法。将四边形的四个角剪下来，将同一个顶点拼在一起，看是否成一个周角。

方法三：拆分法。把四边形分成两个三角形，再用一个三角形内角和180度乘以2就等于360度。

在这个探究过程中，引导学生进行测量，剪拼和拆分的方法，鼓励学生大胆想象，积极思考，为更好地探究多边形内角和做铺垫。

二、动手操作，类比推理。

学生任选一种方式，小组内操作探究五边形的内角和规律。学生任意画一个五边形，然后组内进行探讨，这个五边形的内角和可以根据四边形的三种方法进行类比分析。小组代表在全班汇报，总结出求五边形内角和最好的方法是分为拆分法，用180度×3=540°之后教师用多媒体呈现出六边形，七边形，八边形等，让学生用分割法将这些图形分成若干个三角形，来求出他们的内角和。（在组内探究过程中，自主完成以下学习单）如下图：

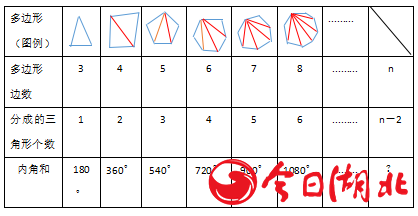
三、探究方法，总结公式。

学生通过表格不难发现多边形分成的三角形个数始终比边数少2，再用三角形个数乘以180°，即为多边形内角和。之后，在教师引导下总结出：n边形内角和等于（n－2）×180°（n≥3的整数）

四、巩固练习，内化新知。

问题1：十边形的内角和是多少度？

问题2：一个多边形的内角和是1800度，这个多边形是几边形？

问题3：一个多边形的每个内角都是120度，它是几边形？

这一环节通过层次递进，由易到难，逐步深入，让学生进行多边形内角和公式的灵活运用，达到举一反三，创新思维的效果。

总之，本课探究多边形的内角和公式是以三角形为基础，通过对四边形，五边形，六边形等等的观察，分割成三角形进行交流，探究，猜想，最后验证，从而获得多边形的内角和公式＝（n－2）×180°，渗透给学生由特殊到一般转换化归的数学思想。进一步提高了学生对几何公式探究的严密逻辑推理能力。教师引导学生通过不断发现问题、提出问题、分析问题和解决问题，增强了学生自主参与教学活动的意识，加强师生、生生之间的合作与交流，不仅让学生在快乐中获得新的数学知识，更让学生积累了更加丰富的数学活动经验。

编辑：晓颖